机器学习-学习笔记(一) –> （假设空间 & 版本空间）及 归纳偏好_在线工具

一、机器学习概念

啥是机器学习

机器学习：假设用P来评估计算机程序在某任务类T上的性能，若一个程序通过利用经验E在T中任务上获得了性能改善，则关于T和P，该程序对E进行了学习
通俗讲：通过计算的方式，利用经验来改善系统自身性能
研究主要内容：“学习算法”--> 从数据中产生模型的算法

---

基本术语

1. 模型（model）：全局性结果；模式（mode）：局部性结果
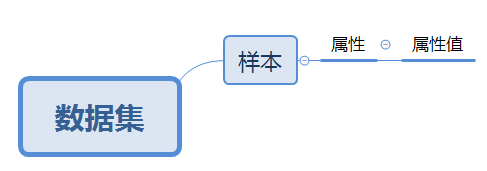
2. 数据集（data set）：记录的集合（机器学习开源数据集）
3. 样本（sample）、示例（instance）：关于一个事件或对象的描述
4. 属性（attribute）、特征（feature）：事件或对象在某方面的表现或性质
5. 属性值（attribute value）：属性的取值
6. 属性空间（attribute space）、样本空间（sample space）：属性作为坐标轴张成的空间
   
7. 特征向量（feature vector）：一个样本在样本空间中对应的坐标向量
8. 维数（dimensionnality）:属性的个数
9. 学习（learning）、训练（training）：从数据中学得模型的过程
10. 标记（label）：关于示例结果的信息
11. 样例（example）：拥有了标记信息的示例
12. 标记空间（label space）：所有标记的集合
13. 训练（training）、学习（learning）：从数据中学得模型的过程
14. 测试（testing）：使用训练得出的模型，对结果进行预测的过程
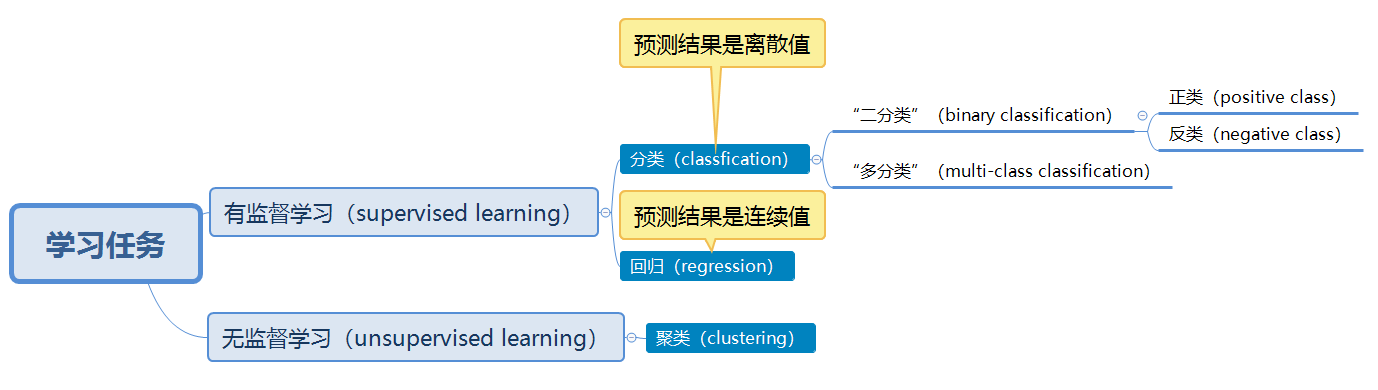
15. 学习任务：
16. 泛化能力（generalization ability）：训练得到的模型适用于测试样本的能力

• 归纳（induction）：特殊到一般
• 演绎（deduction）：一般到特殊的“特化”（specialization）

17. 独立同分布（independent and identically distributed）：获得的每个样本都是从这个分布上采样获得的

---

二、假设空间 & 版本空间

学习过程就是在假设空间中进行搜索的过程，搜索的目标是找到与训练集匹配的假设。

假设空间（hypothesis space）：

1. 假设空间的定义

• 标准定义是：由输入空间到输出空间的映射的集合；
• 我所理解的是：假设空间由三部分组成
  (1) 输入的训练数据集中，每一个属性的所有取值分别组合形成所有可能性结果的集合
  (2) 属性取值至少含一个为“无论去什么值都合适”（即属性值为通配符“*”）的结果集合
  (3) 所有属性值都无法取到的结果，即为空集，一个假设空间有且仅有一个(若训练集中包含正例，则在版本空间中，空集的假设不存在)

2. 假设空间的生成

　　这里通过《机器学习》周志华原著中表1.1的示例进行阐述。
　　　

　　(1) 每一个属性的所有取值分别组合形成所有可能性结果。
　　　　“色泽” ： “青绿”、“乌黑”
　　　　“根蒂” ： “蜷缩”、“硬挺”、“稍蜷”
　　　　“敲声” ： “浊响”、“清脆”、“沉闷”
　　　　总共结果个数：\(2*3*3 = 18\)

色泽＝青绿，根蒂＝蜷缩，敲声＝浊响 色泽＝青绿，根蒂＝蜷缩，敲声＝清脆 色泽＝青绿，根蒂＝蜷缩，敲声＝沉闷 色泽＝青绿，根蒂＝硬挺，敲声＝浊响 色泽＝青绿，根蒂＝硬挺，敲声＝清脆 色泽＝青绿，根蒂＝硬挺，敲声＝沉闷 色泽＝青绿，根蒂＝稍蜷，敲声＝浊响 色泽＝青绿，根蒂＝稍蜷，敲声＝清脆 色泽＝青绿，根蒂＝稍蜷，敲声＝沉闷 色泽＝乌黑，根蒂＝蜷缩，敲声＝浊响 色泽＝乌黑，根蒂＝蜷缩，敲声＝清脆 色泽＝乌黑，根蒂＝蜷缩，敲声＝沉闷 色泽＝乌黑，根蒂＝硬挺，敲声＝浊响 色泽＝乌黑，根蒂＝硬挺，敲声＝清脆 色泽＝乌黑，根蒂＝硬挺，敲声＝沉闷 色泽＝乌黑，根蒂＝稍蜷，敲声＝浊响 色泽＝乌黑，根蒂＝稍蜷，敲声＝清脆 色泽＝乌黑，根蒂＝稍蜷，敲声＝沉闷 

　　(2) 属性取值至少含一个为“无论去什么值都合适”（即属性值为通配符“*”）的结果集合
　　　　“色泽” ： “*”，“青绿”、“乌黑”
　　　　“根蒂” ： “*”，“蜷缩”、“硬挺”、“稍蜷”
　　　　“敲声” ： “*”，“浊响”、“清脆”、“沉闷”
　　　　总共结果个数：\(3*4*4-18 = 30\) (要减去不含*的项)

色泽＝*，   根蒂＝*，   敲声＝* 色泽＝*，   根蒂＝*，   敲声＝浊响 色泽＝*，   根蒂＝*，   敲声＝清脆 色泽＝*，   根蒂＝*，   敲声＝沉闷 色泽＝*，   根蒂＝蜷缩，敲声＝* 色泽＝*，   根蒂＝蜷缩，敲声＝浊响 色泽＝*，   根蒂＝蜷缩，敲声＝清脆 色泽＝*，   根蒂＝蜷缩，敲声＝沉闷 色泽＝*，   根蒂＝硬挺，敲声＝* 色泽＝*，   根蒂＝硬挺，敲声＝浊响 色泽＝*，   根蒂＝硬挺，敲声＝清脆 色泽＝*，   根蒂＝硬挺，敲声＝沉闷 色泽＝*，   根蒂＝稍蜷，敲声＝* 色泽＝*，   根蒂＝稍蜷，敲声＝浊响 色泽＝*，   根蒂＝稍蜷，敲声＝清脆 色泽＝*，   根蒂＝稍蜷，敲声＝沉闷 色泽＝青绿，根蒂＝*，   敲声＝* 色泽＝青绿，根蒂＝*，   敲声＝浊响 色泽＝青绿，根蒂＝*，   敲声＝清脆 色泽＝青绿，根蒂＝*，   敲声＝沉闷 色泽＝青绿，根蒂＝蜷缩，敲声＝* 色泽＝青绿，根蒂＝硬挺，敲声＝* 色泽＝青绿，根蒂＝稍蜷，敲声＝* 色泽＝乌黑，根蒂＝*，   敲声＝* 色泽＝乌黑，根蒂＝*，   敲声＝浊响 色泽＝乌黑，根蒂＝*，   敲声＝清脆 色泽＝乌黑，根蒂＝*，   敲声＝沉闷 色泽＝乌黑，根蒂＝蜷缩，敲声＝* 色泽＝乌黑，根蒂＝硬挺，敲声＝* 色泽＝乌黑，根蒂＝稍蜷，敲声＝* 

　　(3) 所有属性值都无法取到的结果，即为空集，一个假设空间有且仅有一个
　　　　“色泽” ： “Ø”
　　　　“根蒂” ： “Ø”
　　　　“敲声” ： “Ø”
　　　　总共结果个数：1

色泽＝Ø，根蒂＝Ø，敲声＝Ø 

综上所述，假设空间规模大小为
　　\(18+30+1=49\)
　　\((2+1)*(3+1)*(3+1)+1=49\)
　　(色泽两种取值，根蒂三种取值，敲声三种取值，再分别加上通配符，相乘后，加上Ø取值)

版本空间（version space）：

1. 版本空间的定义

• 标准定义：一个与训练集一致的“假设集合”
• 我的理解是：版本空间是假设空间的子集，包含两个部分
  (1)与正例一致的假设
  (2)与反例不一致的假设

2. 版本空间的生成

完整的假设空间：（共49条）

色泽＝青绿，根蒂＝蜷缩，敲声＝浊响 色泽＝青绿，根蒂＝蜷缩，敲声＝清脆 色泽＝青绿，根蒂＝蜷缩，敲声＝沉闷 色泽＝青绿，根蒂＝硬挺，敲声＝浊响 色泽＝青绿，根蒂＝硬挺，敲声＝清脆 色泽＝青绿，根蒂＝硬挺，敲声＝沉闷 色泽＝青绿，根蒂＝稍蜷，敲声＝浊响 色泽＝青绿，根蒂＝稍蜷，敲声＝清脆 色泽＝青绿，根蒂＝稍蜷，敲声＝沉闷 色泽＝乌黑，根蒂＝蜷缩，敲声＝浊响 色泽＝乌黑，根蒂＝蜷缩，敲声＝清脆 色泽＝乌黑，根蒂＝蜷缩，敲声＝沉闷 色泽＝乌黑，根蒂＝硬挺，敲声＝浊响 色泽＝乌黑，根蒂＝硬挺，敲声＝清脆 色泽＝乌黑，根蒂＝硬挺，敲声＝沉闷 色泽＝乌黑，根蒂＝稍蜷，敲声＝浊响 色泽＝乌黑，根蒂＝稍蜷，敲声＝清脆 色泽＝乌黑，根蒂＝稍蜷，敲声＝沉闷 色泽＝*，   根蒂＝*，   敲声＝* 色泽＝*，   根蒂＝*，   敲声＝浊响 色泽＝*，   根蒂＝*，   敲声＝清脆 色泽＝*，   根蒂＝*，   敲声＝沉闷 色泽＝*，   根蒂＝蜷缩，敲声＝* 色泽＝*，   根蒂＝蜷缩，敲声＝浊响 色泽＝*，   根蒂＝蜷缩，敲声＝清脆 色泽＝*，   根蒂＝蜷缩，敲声＝沉闷 色泽＝*，   根蒂＝硬挺，敲声＝* 色泽＝*，   根蒂＝硬挺，敲声＝浊响 色泽＝*，   根蒂＝硬挺，敲声＝清脆 色泽＝*，   根蒂＝硬挺，敲声＝沉闷 色泽＝*，   根蒂＝稍蜷，敲声＝* 色泽＝*，   根蒂＝稍蜷，敲声＝浊响 色泽＝*，   根蒂＝稍蜷，敲声＝清脆 色泽＝*，   根蒂＝稍蜷，敲声＝沉闷 色泽＝青绿，根蒂＝*，   敲声＝* 色泽＝青绿，根蒂＝*，   敲声＝浊响 色泽＝青绿，根蒂＝*，   敲声＝清脆 色泽＝青绿，根蒂＝*，   敲声＝沉闷 色泽＝青绿，根蒂＝蜷缩，敲声＝* 色泽＝青绿，根蒂＝硬挺，敲声＝* 色泽＝青绿，根蒂＝稍蜷，敲声＝* 色泽＝乌黑，根蒂＝*，   敲声＝* 色泽＝乌黑，根蒂＝*，   敲声＝浊响 色泽＝乌黑，根蒂＝*，   敲声＝清脆 色泽＝乌黑，根蒂＝*，   敲声＝沉闷 色泽＝乌黑，根蒂＝蜷缩，敲声＝* 色泽＝乌黑，根蒂＝硬挺，敲声＝* 色泽＝乌黑，根蒂＝稍蜷，敲声＝* 色泽＝Ø，根蒂＝Ø，敲声＝Ø 

　　(1) 删除与正例不一致的假设。
　　　　正例1：色泽＝青绿，根蒂＝蜷缩，敲声＝浊响，好瓜=是

要删除的项：（41项） 2.	色泽＝青绿，根蒂＝蜷缩，敲声＝清脆 3.	色泽＝青绿，根蒂＝蜷缩，敲声＝沉闷 4.	色泽＝青绿，根蒂＝硬挺，敲声＝浊响 5.	色泽＝青绿，根蒂＝硬挺，敲声＝清脆 6.	色泽＝青绿，根蒂＝硬挺，敲声＝沉闷 7.	色泽＝青绿，根蒂＝稍蜷，敲声＝浊响 8.	色泽＝青绿，根蒂＝稍蜷，敲声＝清脆 9.	色泽＝青绿，根蒂＝稍蜷，敲声＝沉闷 10.	色泽＝乌黑，根蒂＝蜷缩，敲声＝浊响 11.	色泽＝乌黑，根蒂＝蜷缩，敲声＝清脆 12.	色泽＝乌黑，根蒂＝蜷缩，敲声＝沉闷 13.	色泽＝乌黑，根蒂＝硬挺，敲声＝浊响 14.	色泽＝乌黑，根蒂＝硬挺，敲声＝清脆 15.	色泽＝乌黑，根蒂＝硬挺，敲声＝沉闷 16.	色泽＝乌黑，根蒂＝稍蜷，敲声＝浊响 17.	色泽＝乌黑，根蒂＝稍蜷，敲声＝清脆 18.	色泽＝乌黑，根蒂＝稍蜷，敲声＝沉闷 21.	色泽＝*，   根蒂＝*，   敲声＝清脆 22.	色泽＝*，   根蒂＝*，   敲声＝沉闷 25.	色泽＝*，   根蒂＝蜷缩，敲声＝清脆 26.	色泽＝*，   根蒂＝蜷缩，敲声＝沉闷 27.	色泽＝*，   根蒂＝硬挺，敲声＝* 28.	色泽＝*，   根蒂＝硬挺，敲声＝浊响 29.	色泽＝*，   根蒂＝硬挺，敲声＝清脆 30.	色泽＝*，   根蒂＝硬挺，敲声＝沉闷 31.	色泽＝*，   根蒂＝稍蜷，敲声＝* 32.	色泽＝*，   根蒂＝稍蜷，敲声＝浊响 33.	色泽＝*，   根蒂＝稍蜷，敲声＝清脆 34.	色泽＝*，   根蒂＝稍蜷，敲声＝沉闷 37.	色泽＝青绿，根蒂＝*，   敲声＝清脆 38.	色泽＝青绿，根蒂＝*，   敲声＝沉闷 40.	色泽＝青绿，根蒂＝硬挺，敲声＝* 41.	色泽＝青绿，根蒂＝稍蜷，敲声＝* 42.	色泽＝乌黑，根蒂＝*，   敲声＝* 43.	色泽＝乌黑，根蒂＝*，   敲声＝浊响 44.	色泽＝乌黑，根蒂＝*，   敲声＝清脆 45.	色泽＝乌黑，根蒂＝*，   敲声＝沉闷 46.	色泽＝乌黑，根蒂＝蜷缩，敲声＝* 47.	色泽＝乌黑，根蒂＝硬挺，敲声＝* 48.	色泽＝乌黑，根蒂＝稍蜷，敲声＝* 49.	色泽＝Ø，根蒂＝Ø，敲声＝Ø 

删除后剩余项：（8项） 1.	色泽＝青绿，根蒂＝蜷缩，敲声＝浊响 19.	色泽＝*，   根蒂＝*，   敲声＝* 20.	色泽＝*，   根蒂＝*，   敲声＝浊响 23.	色泽＝*，   根蒂＝蜷缩，敲声＝* 24.	色泽＝*，   根蒂＝蜷缩，敲声＝浊响 35.	色泽＝青绿，根蒂＝*，   敲声＝* 36.	色泽＝青绿，根蒂＝*，   敲声＝浊响 39.	色泽＝青绿，根蒂＝蜷缩，敲声＝* 

　　　　正例2：色泽＝乌黑，根蒂＝蜷缩，敲声＝浊响，好瓜=是

要删除的项：（4项） 1.	色泽＝青绿，根蒂＝蜷缩，敲声＝浊响 35.	色泽＝青绿，根蒂＝*，   敲声＝* 36.	色泽＝青绿，根蒂＝*，   敲声＝浊响 39.	色泽＝青绿，根蒂＝蜷缩，敲声＝* 

删除后的剩余项：（4项） 19.	色泽＝*，   根蒂＝*，   敲声＝* 20.	色泽＝*，   根蒂＝*，   敲声＝浊响 23.	色泽＝*，   根蒂＝蜷缩，敲声＝* 24.	色泽＝*，   根蒂＝蜷缩，敲声＝浊响 

　　(1) 删除与反例一致的假设。
　　　　反例1：色泽＝青绿，根蒂＝硬挺，敲声＝清脆，好瓜=否

要删除的项：（1项） 19.	色泽＝*，   根蒂＝*，   敲声＝* 

删除后的剩余项：（3项） 20.	色泽＝*，   根蒂＝*，   敲声＝浊响 23.	色泽＝*，   根蒂＝蜷缩，敲声＝* 24.	色泽＝*，   根蒂＝蜷缩，敲声＝浊响 

　　　　反例2：色泽＝乌黑，根蒂＝稍蜷，敲声＝沉闷，好瓜=否

要删除的项：（0项） 

最终得到的版本空间：

20.	色泽＝*，   根蒂＝*，   敲声＝浊响 23.	色泽＝*，   根蒂＝蜷缩，敲声＝* 24.	色泽＝*，   根蒂＝蜷缩，敲声＝浊响 

---

三、归纳偏好

归纳偏好（inductive bias）的定义

• 标准定义：机器学习算法在学习过程中，对某种类型假设的偏好，称为归纳偏好。
• 我所理解的是：在版本空间所产生的假设集合中，哪一个假设是在版本空间中更好的假设，则在之后的测试过程中选择时，更偏向于哪个。

任何一个有效的机器学习算法必有其归纳偏好。若其不存在归纳偏好，则训练集中假设都“等效”，则在测试过程中，训练集的假设随机选择，得到的结果时好时坏，产生波动，则结果无意义。

“奥卡姆剃刀”（Occam's razor）原则

若有多个假设与观察一致，则选择最简单的那个（使模型结构尽量简单）。

其实，并不能完全遵循“奥卡姆剃刀”原则，因为对于“模型哪个更简单？”的定义是模糊的，并没有一个确切的标准说哪个模型最简单，并且最简单的模型一定与问题密切相关。所以，算法的归纳偏好是否与问题本身相匹配，更直接决定了算法是否取得更好的性能。

“没有免费的午餐定理”（No Free Lunch Theorem）

1. 定理内容

• 标准定义：无论学习算法A多聪明，学习算法B多笨拙，他们的期望性能相同。
  重要前提：所有问题出现的机会相同、或所有问题同等重要。
• 我所认为其本质想阐述的是：一个适合于某问题的算法，在另一个问题上不一定适合。
  其实我们在解决问题的时候，更关注于问题本身，，就当前问题提出解决方法，在存在可能性的范围内实现“举一反三”的泛化，而非一味的将当前问题的解决方案适用于其他问题，或者找出两个及以上弱相关问题之间的通解。

2. 公式推导

这里的三个公式主要为了证明学习算法\(ε_a\)与\(ε_b\)在训练集之外的所有样本上（测试数据集）的误差之和即总误差与学习算法无关。即对任意的学习算法，其总误差相等。
(根据《机器学习》周志华原著公式1.1，1.2，1.3来解释)

公式1.1：

(1)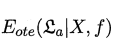 : 表示学习算法\(ε_a\)在训练集之外的所有样本上的误差，也即被预测样本(测试样本)上的误差。（ote：off-training error）
我认为这里的样本应该包括两部分：训练样本和测试样本，训练样本用于学习得出模型，测试样本则用来判断模型是否与问题相匹配。所以，判断与测试样本的误差，可以确定学习算法的好坏。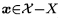
：就表示\(x\)属于整个样本空间减去训练样本，即\(x\)属于测试样本空间，是测试样本空间的其中一项。
(2)\(P(x)\)：表示\(x\)在整个样本空间中出现的概率
例如：（这里的举例有待考究，还望指正）
色泽=*，根蒂=蜷缩，敲声=浊响 在下面的样本空间中，\(P(x)=3/3=1\)
色泽=*，根蒂=稍蜷，敲声=浊响 在下面的样本空间中，\(P(x)=1/3\)

色泽＝*，   根蒂＝*，   敲声＝浊响 色泽＝*，   根蒂＝蜷缩，敲声＝* 色泽＝*，   根蒂＝蜷缩，敲声＝浊响 

(3)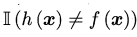：指示函数，若\(h(x)≠f(x)\)则为1，否则为0，即表示学习算法基于训练数据产生的假设是否符合目标函数。
(4)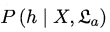：表示算法\(ε_a\)基于训练数据\(X\)产生假设\(h\)的概率。因为算法\(ε_a\)在训练数据\(X\)上训练时，产生多种假设，存在其中一种假设\(h\)在训练数据\(X\)上的条件概率，并且，由算法\(ε_a\)基于训练数据\(X\)产生的所有假设的条件概率总和为1。(TODO：这里的解释可能需要修改)
(5)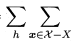：因为样本空间和假设空间是离散的，所以这里采用求和，而非连续的求积分。
根据条件期望公式，即可得出该式。

---

公式1.2

(1)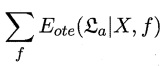：表示对所有可能的目标函数\(f\)按均匀分布对误差求和。
只要满足版本空间\(χ\)的假设函数，都可以是目标函数，所以目标函数\(f\)可能不止一个。因为每一个目标函数\(f\)均匀分布，且是二分类问题(即每一个样本，都会有两个不同的目标函数\(f\))，所以对于有\(|χ|\)个样本的版本空间，则会有\(2^{|χ|}\)个目标函数，但是因为有一半的目标函数\(f\)对\(x\)的预测与\(h(x)\)不一致，即某个假设\(h\)有\(\frac{1}{2}\)的概率与目标函数\(f\)相同。(我认为可以类比满二叉树，树高为\(|χ|\)，则树中结点总数为\({1} \over {2}\)\(2^{|χ|}\))
故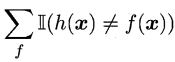\(=\)\({1} \over {2}\)\(2^{|χ|}\)
举例：
若样本空间\(χ=\{x_1, x_2\}\)，则\(|χ|=2\)，所有可能的目标函数\(f\)为：
\(f_1: f_1(x_1)=0,f_1(x_2)=0\)
\(f_2: f_2(x_1)=0,f_2(x_2)=1\)
\(f_3: f_3(x_1)=1,f_3(x_2)=0\)
\(f_4: f_4(x_1)=1,f_4(x_2)=1\)
则总共有\(2^{|χ|}=2^2=4\)个目标函数\(f\)。
若学习产生的假设\(h(x_1)=0\)，则仅有\({1}\over{2}\)的\(f\)与之相等，即\(f_1\)和\(f_2\).
所以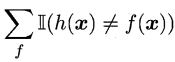：\(=\)\({1} \over {2}\)\(2^{|χ|}\)\(=2\)
(2)
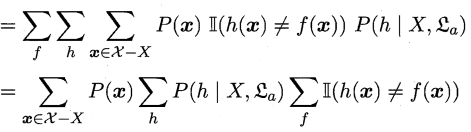
这一步其实就是一个求和运算
\((a_1+a_2+...+a_x)(b_1+b_2+...+b_y)(c_1+c_2+...+c_z)=a_1b_1c_1+a_1b_1c_2+...+a_1b_1c_z+a_1b_2c_1+...+a_xb_yc_z\)
(3)
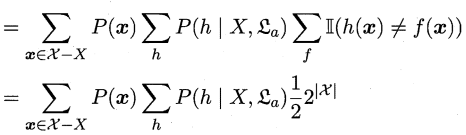
这一步在(1)中已经做过解释
(4)
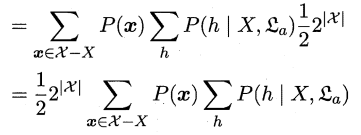
这一步其实就是提取公因式
(5)
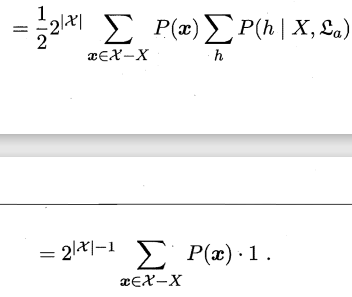
这一步是因为由算法\(ε_a\)基于训练数据\(X\)产生的所有假设的条件概率总和为1
不难看出，所有可能的目标函数\(f\)的总误差与算法\(ε_a\)并无关系

---

公式1.3

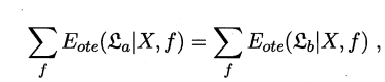
在所有可能的目标函数\(f\)均匀分布的前提下(即问题出现的机会相等，所有问题同等重要)，无论学习算法\(ε_a\)多聪明，\(ε_b\)多笨拙，他们的期望性能(总误差)相同。
但其实，我们只是假设目标函数\(f\)服从均匀分布。而真正情况是，对于某一种问题，只有与已有的样本数据或者现有问题高度拟合的函数，才是真正的目标函数，要实际问题具体分析。
所以，学习算法与问题的契合程度才是衡量学习算法优劣的决定性因素。

---

四、发展历程

机器学习的发展历程在Eren Golge博客中用一张图具体阐明了，在此借鉴引用。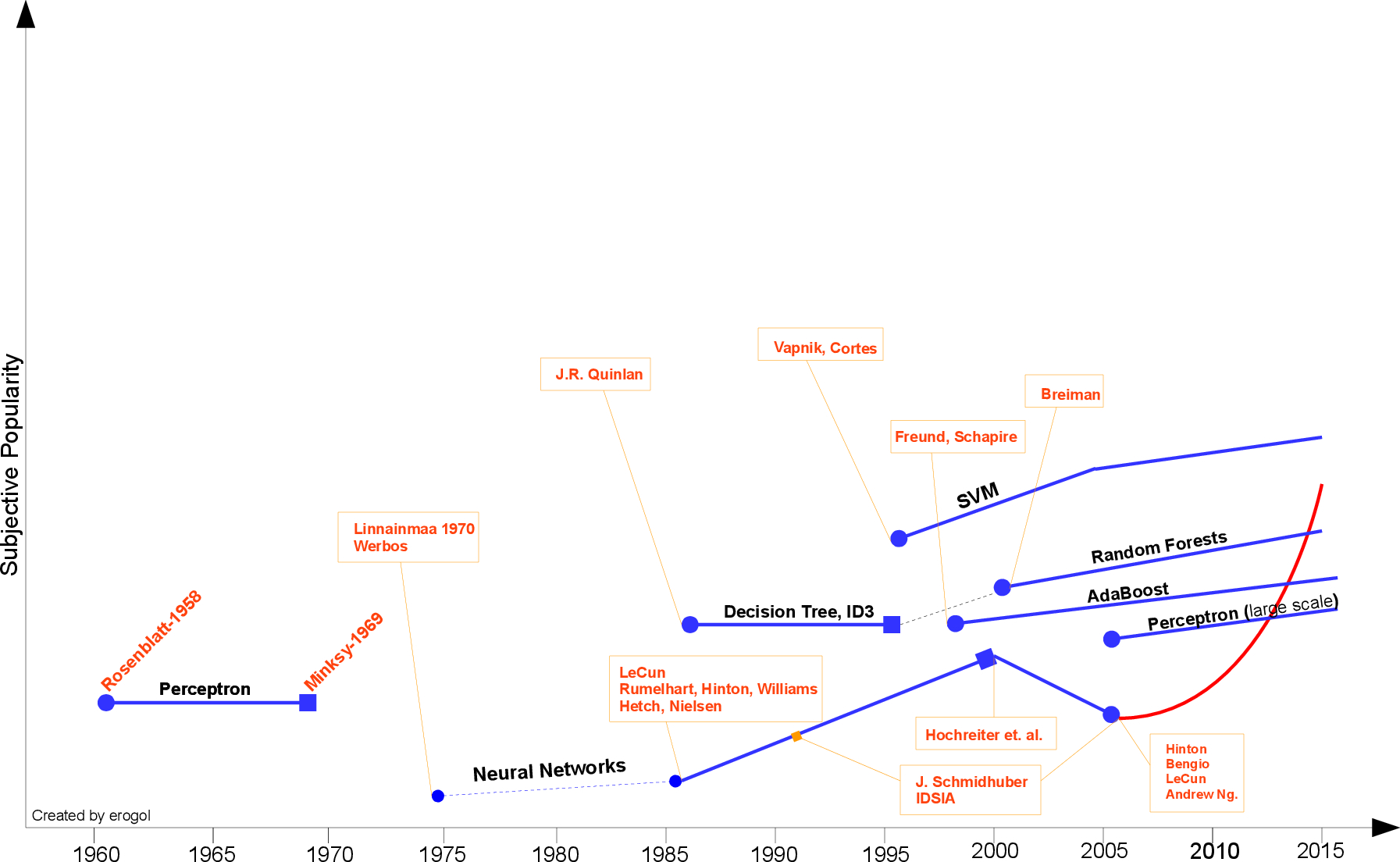

---

五、应用现状

（ps：本文完全是个人学习笔记，其中引用了“西瓜书”“南瓜书”的内容，对其进行理解和解释，若有问题或错误，希望各位前辈进行指正）